Teorema Di Taylor Con Resto Di Peano
Teorema Di Taylor Con Resto Di Peano. Teoremi sulle derivate rapporto incrementale e derivata prima maplet con animazione sull'interpretazione geometrica della. Teorema (formula di taylor locale, con il resto di peano) in particolare, se x0 = 0, si ha la formula (detta di maclaurin) teorema (formula di taylor con il resto di lagrange). Ultimo video prima di buttarci nella risoluzione degli esercizi di spiegazione ed ulteriore chiarimento sugli sviluppi di taylor insieme al principio di sostituzione degli infinitesimi usati per la risoluzione di limiti presentanti la forma indeterminata 0/0. Il teorema di taylor con il resto nella forma di peano (che ora dimostriamo) aerma che la. Fissiamo un punto x0 in i.
Sia f (x) una funzione derivabile n volte in un x0, allora in un intorno di x0 risulta. • o(x − x0)n si chiama il resto in forma di peano. Il teorema di taylor, in analisi matematica, è un teorema che fornisce una sequenza di approssimazioni di una funzione differenziabile attorno ad un dato punto mediante i polinomi di taylor, i cui coefficienti dipendono solo dalle derivate della funzione nel punto. Teorema di cauchy e lagrange. Fissiamo un punto x0 in i.
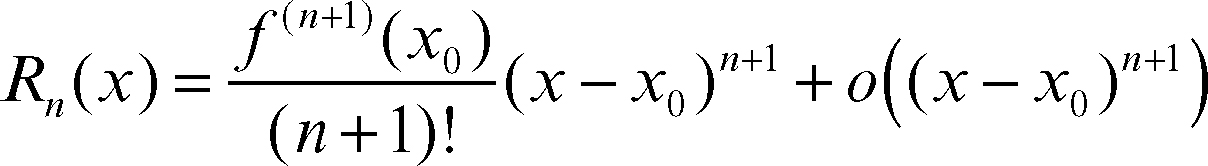
Il seguente teorema (che generalizza il teorema del valore medio di lagrange) `e di carattere globale:
9 esercizi sui polinomi di taylor calcolare i seguenti polinomi di taylor con centro in 0, usando ove possibile i polinomi di esercizi con i teoremi di de l hôpital e la formula di taylor. Il teorema di taylor, in analisi matematica, è un teorema che fornisce una sequenza di approssimazioni di una funzione differenziabile attorno ad un dato punto mediante i polinomi di taylor, i cui coefficienti dipendono solo dalle derivate della funzione nel punto. Teorema 1.1 (formula di taylor con resto di peano). 51:16 in questa lezione viene enunciata e spiegata la nota formula di taylor rispettivamente con resto di lagrange e poi di peano ed successivamente viene svolto un esempio proprio sull'applicazione della formula di mclaurin con l'utilizzo del resto di. La formula di taylor con resto di peano.
Teorema (formula di taylor locale, con il resto di peano) in particolare, se x0 = 0, si ha la formula (detta di maclaurin) teorema (formula di taylor con il resto di lagrange). Il teorema di taylor, in analisi matematica, è un teorema che fornisce una sequenza di approssimazioni di una funzione differenziabile attorno ad un dato punto mediante i polinomi di taylor, i cui coefficienti dipendono solo dalle derivate della funzione nel punto. Il resto di peano una funzione f definita in un intorno di un punto x0 si dice derivabile in x0 se e solo se. Formula di taylor resto di lagrange e resto di peano 70. Dierenza tra la funzione f (x) e il teorema 1.2 (formula di taylor con il resto di peano) sia f una funzione di classe cn su un intervallo aperto i dell'asse reale.

Teorema di taylor con resto di peano.
Questa formula è di estrema utilità nel calcolo dei limiti. Teorema di rolle, lagrange, cauchy (con le relative dimostrazioni e i significati geometrici) e de l'hôpital. Vediamo cos'è e come si usa la formula di taylor con resto di peano e centro in zero. X→0 xn questa è una forma indeterminata 0/0 possiamo. .del resto nella formula di taylor, l'introduzione della struttura di spazio vettoriale, la 'curva di peano', e il i giochi del libro sono in parte inventati dall'autore stesso, tuttavia sono molti quelli che peano ha ripreso qui si può vedere un teorema di fermat, o lo sviluppo d'una frazione ordinaria in frazione.
9 esercizi sui polinomi di taylor calcolare i seguenti polinomi di taylor con centro in 0, usando ove possibile i polinomi di esercizi con i teoremi di de l hôpital e la formula di taylor. Vediamo inoltre come si possano risolvere limiti con taylor e come. Fissiamo un punto x0 in i. Formula taylor con resto peano (+ crit max/min). Ultimo video prima di buttarci nella risoluzione degli esercizi di spiegazione ed ulteriore chiarimento sugli sviluppi di taylor insieme al principio di sostituzione degli infinitesimi usati per la risoluzione di limiti presentanti la forma indeterminata 0/0.

Il resto di peano una funzione f definita in un intorno di un punto x0 si dice derivabile in x0 se e solo se.
En cálculo diferencial, el teorema de taylor, recibe su nombre del matemático británico, brook taylor, quien lo enunció con mayor generalidad en 1712, aunque previamente james gregory lo había descubierto en 1671. Teorema di rolle, lagrange, cauchy (con le relative dimostrazioni e i significati geometrici) e de l'hôpital. Teorema di cauchy e lagrange. Oddio penserai, ma questo è fuori come una campana stonata! Capitolo 5 teoremi di l'hospital e di taylor.
Posting Komentar untuk "Teorema Di Taylor Con Resto Di Peano"